ما هو قانون مساحة المستطيل

المساحة

تُعَرَّف المساحة بالكمّية التي تمثل الامتداد المحصور في شكل ثنائي الأبعاد. فعندما نقول أنّ مساحة قطعة أرض هي دونم واحد نقصد بذلك أنّ هذه الأرض تغطي امتداداً مقداره دونم واحد أو 1000 متر مربع. لذلك فالوحدة التي تُقاس بها المساحة هي وحدة قياس المسافة (الطول أو العرض مثلاً) مضروبةٌ بنفسها، من هنا كانت وحدة القياس المستخدمة للمساحة في النظام العالمي لوحدات القياس (international system of units) هي المتر المربع (م2).

مساحة الأشكال الهندسية الأساسية

إنّ أبسط الأشكال الهندسية هي تلك التي تأخذ حيِّزاً ثنائيَّ الأبعاد، مثل المربع، المستطيل، المثلث، والدائرة.

المربع، هو شكل رباعي الأضلاع تكون كل أضلاعه متساوية الطول، وتعطى مساحته بتربيع طول ضلعه أو بضرب طول الضلع بنفسه. فمثلاً مساحة المربع الذي طول ضلعه 10 سنتيمترات (سم) هي (10 ^ 2) أو (10 * 10) وتساوي 100 سنتيمتراً مربَّعاً. إذن: مساحة المربع = الضلع × الضلع.

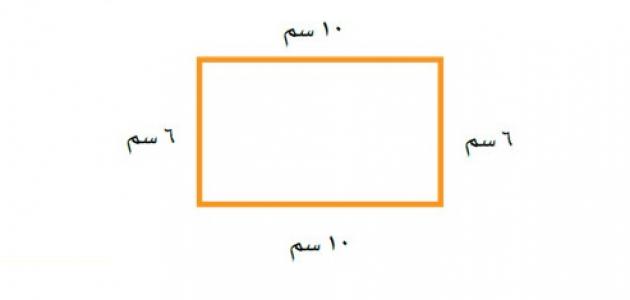
المستطيل، شكل رباعي الأضلاع يتساوى فيه طول كلّ ضلعين متقابلين، ويُسَمّى أحد الضلعين الطول أمّا أحد الضلعين الآخرين فيُسمّى العرض. وتُعطى مساحة المستطيل بحاصل ضرب الطول في العرض. وكذلك: مساحة المستطيل = الطول × العرض.

المثلث، وهو شكل ثلاثي الأضلاع تختلف تسميته باختلاف نسبة أطوال أضلاعه إلى بعضها، فهناك المثلث متساوي الساقين والمثلث متساوي الأضلاع. أمّا مساحة المثلث فتُحسبُ بنصف حاصل ضرب القاعدة بالإرتفاع، أمّا القاعدة فهي أحد أضلاع المثلث ويكون الارتفاع هو المسافة من تلك القاعدة إلى رأس المثلث. من هنا يمكن أن نقول: مساحة المثلث = (1\2) × القاعدة × الارتفاع.

الدائرة، وهي عبارة عن شكلٍ منحنٍ مغلق على نفسه تكون فيه المسافة بين أي نقطةٍ على ذلك المنحنى ومركز الدائرة دائما ثابتة وتُسمَّى بنصف قطر الدائرة. ولحساب مساحة الدائرة هناك قيمة رياضية تستخدم في الهندسة وهي النسبة الدائرية (π - pi) والذي يساوي تقريباً (22\7). ومساحة الدائرة = (1\2) × (π ) × (نصف القطر × نصف القطر).

وحدات قياس المساحة

كما ذكرنا سابقاً فالوحدة العالمية لقياس المساحة هي المتر المربع، إلّا أنّ وحدات مختلفة تستخدم لقياس المساحة مثل:

• الدونم ويساوي 1000 متر مربع.
• الفدّان ويساوي تقريباً 4200 متر مربع.
• الهكتار ويساوي 10000 متر مربع.
• الكيلو متر المربع وهو 1000000 متر مربع.

الوحدات السابقة تستخدم غالباً لقياس مساحة الأراضي بمختلف أنواعها.

وحدات قياس أخرى

هناك وحداتٌ أخرى تستخدم لقياس المساحات الصغيرة مثل:

• السنتيمتر المربع وهو جزءٌ من المتر المربع ويساوي 0،0001 من المتر المربع.
• الملليمتر المربع وهو أصغر من السنتيمتر المربع ويساوي 0،000001 من المتر المربع.

وهناك العديد من وحدات قياس المساحة التي تختلف باختلاف استخداماتها.