كيفية حساب محيط المستطيل

حساب محيط المستطيل

المستطيل: هو أحد الأشكال الهندسية الأكثر استخداماً في الهندسة و في كل ما يتعلق بها و في كل التطبيقات التي تحتاج إليه سواء الهندسية أو غير الهندسية، إذ إن العديد من التصاميم تعتمد و بشكل أساسي على الهندسة و من هنا فإنه لا يمكن البتة استثناء المستطيلات أو إهمالها و لا بأي حال من الأحوال، فإهمال القوانين التي تستخدم لتحليل و تصميم المستطيلات سيعمل على تضييع الهدف المرجو من هذا المستطيل. و يمكن النظر إلى المستطيل على أنه حالة من حالات متوازي الأضلاع ( حالة خاصة ) لأن كل ضلعين متقابلين في المستطيل هما متوازيان، و من هنا فإنه يحقق شرط متوازي الأضلاع و ما يجعله حالة خاصة هو أن جميع زواياه قائمة ( 90 درجة ) في حين يمكن اعتبار أن المربع هو إحدى حالات المستطيل الخاصة و الذي تكون جميع أضلاعه متساوية و جميع زواياه قائمة أيضاً.

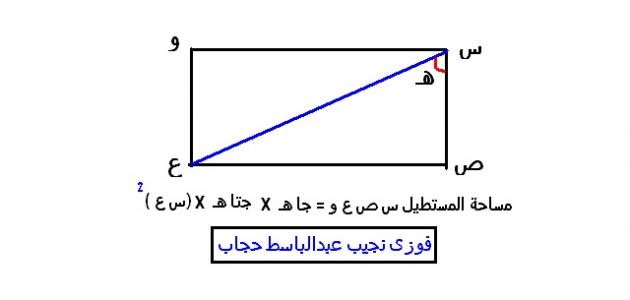
الضلع الأطول في المستطيل يسمى طول المستطيل أما الضلع الأقصر فهو عرض المستطيل. و من خصائصه أن كل ضلعين متقابلين في المستطيل هما متوازيين و متساويين، و بناء على أن جميع زوايا المستطيل قائمة، و من هنا يمكننا أن نحسب طول قطر المستطيل وقطر المستطيل هو الخط الواصل ما بين كل زاويتين متقابلتين من زوايا المستطيل. ويمكن حساب ذلك باستخدام نظرية فيثاغورس والتي تنص على أن وتر المثلث قائم الزاوية يساوي الجذر التربيعي لمجموع مربعي الضلعين الآخرين.

يمكن حساب مساحة المستطيل عن طريق إيجاد حاصل ضرب طوله في عرضه، كما و يمكن إيجاد محيط المستطيل بإيجاد مجموع أطواله الأربعة. والمثال التالي سيوضح عملياً طريقة حساب كافة القيم السابقة.

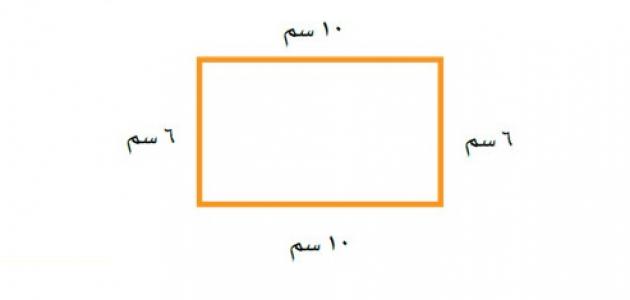
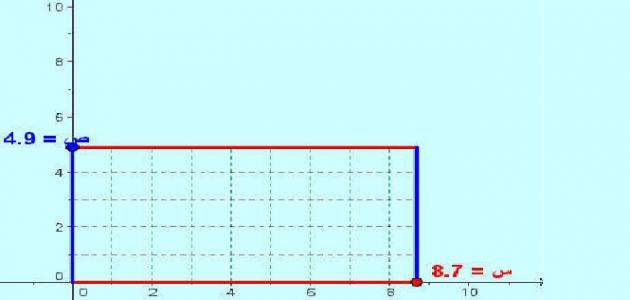
مثال: مستطيل طوله يساوي 10 سم و عرضه يساوي 7 سم والمطلوب هو إيجاد مساحته ومحيطه وطول قطره. ولنبدأ بالترتيب، فبناءً على ما سبق فإن مساحة المستطيل = الطول x العرض = 10 سم x 7 سم = 70 سم مربع، أما محيط المستطيل = 10 x 2 + 7 x 2 = ( 10 + 7 ) x 2 = 34 سم، وأخيراً يمكن حساب طول قطر المستطيل بإيجاد الجذر التربيعي لمجموع المربعين فمربع الطول = 100 سم مربع أما مربع العرض = 49 سم مربع ومن هنا فطول القطر يساوي الجذر التربيعي لـ 149 سم مربع والذي يساوي 12.2 سم تقريباً.