
محتويات
- ١ الشّكل الرباعيّّ
- ٢ المستطيل
- ٣ قانون مُحيط المستطيل
- ٤ أمثلة على محيط المستطيل
- ٥ مساحة المستطيل
- ٦ أمثلة على مساحة المستطيل
- ٧ متوازي المُستطيلات
- ٨ المراجع
الشّكل الرباعيّّ
الأشكال الرباعيّة (بالإنجليزيّة: Quadrilaterals) هي عبارة عن أشكال ثنائيّة الأبعاد، ذات أربعة أضلاع مُغلقة ومستقيمة، ولهذه الأشكال الرباعيّة أربع زوايا قائمة، وعند جمعها فإنَّ الناتج سيكون 360 درجةً، ومن أشهر الأمثلة على الأشكال الرباعيّة: المُستطيل، ومتوازي الأضلاع، والمُربَّع.[١]
المستطيل
المستطيل هو شكل رباعيّ، كلّ ضلعين متقابلين فيه متوازيان ومتساويان في الطّول، ومجموع زواياه الأربعة يساوي ثلاثمئة وستّين درجةً، وذلك يعني أنّ قياس كلّ زاوية في المستطيل يساوي تسعين درجةً؛ أي إنّ زاوياه جميعها قائمة. يُسمّى الضلع الطّويل في هذا الشّكل الهندسيّ الطّولَ، أمّا الضّلع القصير فيُسمّى العرضَ؛ وهذا ما يميّز المستطيل، فلو كانت أطوال أضلاعه كلّها متساويةً فسيتحوّل إلى شكل آخر وهو المربّع، وفيما يأتي بعض خصائص المستطيل:[٢][٣]
- قُطرا المُستطيل متساويا الطّول.
- قُطرا المستطيل يُنصّف كلّ منهما الآخر.
- كلُّ ضلعَين متقابِلَين في المُستطيل متوازيان.
- كلُّ ضلعَين مُتقابلَينِ في المُستطيل متساويا الطّول.
- المُستطيل هو أحد أشكال متوازي الأضلاع، إلّا أنَّ زواياه قائمة.
قانون مُحيط المستطيل
محيط أيِّ مُضلَّع هو المسافة حولَ هذا المُضلَّع، ويُقاسُ المُحيط بوحداتٍ خطيّةٍ، ويُعدّ أحاديّ الأبعاد رغمَ أنّ المُضلَّع ثُنائيّ الأبعاد،[٤] ولإيجاد مُحيط المُستطيل، يجب جَمع أطوال حدود كُلّ جانب، وذلك عن طريق استخدام قانون مُحيط المُستطيل بأحد أشكاله الآتية:[٥]
- محيط المستطيل=2×(الطول+العرض)
- محيط المستطيل=(2×الطول)+(2×العرض)
- محيط المستطيل=الطول+الطول+العرض+العرض
وباستخدام قانون محيط المستطيل، يمكن حساب محيط المستطيل اعتماداً على طول المُستطيل وعرضه كما في الأمثلة الآتية:[٢]
- مثال (1): مستطيل طوله 16سم، وعرضه 9سم، جِد محيطهُ.
الحلّ: محيط المستطيل=(2×16)+(2×9) محيط المستطيل=50سم
- مثال (2): مستطيل طوله 10سم وعرضه 8سم، جِد محيطهُ.
الحلّ: محيط المستطيل=2×(10+8) محيط المستطيل=36سم
أمثلة على محيط المستطيل
- مثال (1): مُستطيل طوله 7 وحدات، وعرضه 4 وحدات، جِد محيطه.[٥]
الحلّ: باستخدام قانون محيط المستطيل، فإنَّ حساب المحيط له يكون كما يأتي: محيط المستطيل=7+7+4+4 محيط المستطيل=2×7+2×4 محيط المستطيل=22 وحدةً
- مثال (2): مستطيل طوله 8 إنشات، وعرضه 3 إنشات، جِد محيطه.[٤]
الحلّ: بما أنَّ محيط المستطيل يساوي مجموع أطوال أضلاعه، إذاً فالحلّ يكون كما يأتي: محيط المستطيل=3+3+8+8 محيط المستطيل=22 إنشاً
- مثال (3): مستطيل طوله 45م، وعرضه 35م، جِد محيطه.[٦]
الحلّ: بتعويض طول المُستطيل وعرضه في قانون محيط المستطيل، فإنَّ الناتج سيكون كما يأتي: محيط المستطيل=(2×45)+(2×35) محيط المستطيل=160م
- مثال (4): أمَرَ مُدرِّب كُرة القدم اللّاعب سامي بالرّكض حول الملعب 3 دوراتٍ، وكان الملعب مستطيل الشّكل، طوله 160م، وعرضه 53م، جِد المسافة الكُليّة التي سيركضها اللّاعب سامي حول الملعب.[٧]
الحلّ: بما أنَّ سامي سيركض حول الملعب المستطيل، حينها يجب حساب مُحيطه، وبتعويض طول الملعب وعرضه في قانون محيط المستطيل، فإنّ النّاتج سيكون كالآتي: محيط الملعب=(2×160)+(2×53) محيط الملعب=426م بما أنَّ سامي سيركض 3 دوراتٍ، إذاً سيركض مسافةً تساوي ثلاثة أضعاف محيط الملعب، ولهذا فإنّ: مسافة الرّكض الكُليّة=426×3 مسافة الرّكض الكُليّة=1278م
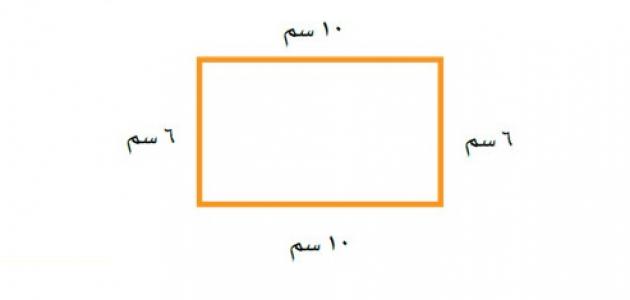
- مثال (5): دخلت نملة غرفة نوم مستطيلة الشّكل ومشت حولها، وكان طول هذه الغرفة 10 أقدام، وعرضها 6 أقدام، جِد المسافة التي قطعتها النّملة.[٧]
الحلّ: بحساب محيط الغرفة، فإنَّ المحيط سيكون مساوياً لما قطعته النّملة؛ لأنّها مشت حول الغرفة: محيط الغرفة=(2×10)+(2×6) محيط الغرفة=32 قدماً
- مثال (6): محيط مستطيلٍ يُساوي 14 إنشاً، أمّا عرضه فيُساوي 4 إنشات، جِد طوله.[٨]
الحلّ: بتعويض المُعطَيات في قانون محيط المستطيل، فالمجهول الوحيد المُتبقّي هو الطّول، وباستخدام أحد قوانين مُحيط المستطيل يمكن إيجاده: محيط المستطيل=(2×الطول)+(2×العرض) 14=(2×الطول)+(2×4) 14=(2×الطول)+8 بنقل الرّقم 8 إلى الجهة الأخرى من المعادلة، فستنعكس إشارته. 14-8=2×الطول 6=2×الطول بقسمة طرفي المعادلة على 2: الطول=3 إنشاتٍ
- مثال (7): مستطيل محيطه 18 إنشاً، وطوله 5 إنشاتٍ، جِد عرضه.[٨]
الحلّ: بتعويض المُعطَيات في قانون محيط المستطيل، فإنّ المجهول الوحيد المُتبقّي في هذه الحالة هو العرض، ويمكن إيجاد قيمته بحلّ المعادلة: محيط المستطيل=(2×الطول)+(2×العرض) 18=(2×5)+(2×العرض) 18=10+(2×العرض) بنقل الرقم 10 إلى الجهة الأخرى من المعادلة، ستنعكس إشارته: 10-18=2×العرض 8=2×العرض بقسمة طرفَي المعادلة على 2: العرض=4 إنشاتٍ
- مثال (8): مستطيل طوله 9سم، وعرضه 5سم، جِد محيطه.[٨]
الحلّ: باستخدام قانون محيط المستطيل: محيط المستطيل=(2×9)+(2×5) محيط المستطيل=18+10 محيط المستطيل=28سم
- مثال (9): مستطيل طوله 5سم وعرضه 3سم، جِد محيطه.[٨]
الحلّ: بالتعويض في قانون محيط المستطيل: محيط المستطيل=(2×5)+(2×3) محيط المستطيل=10+6 محيط المستطيل=16سم
مساحة المستطيل
إنَّ المساحة بشكلٍ عامّ هي عبارة عن عدد الوحدات المُربَّعة داخل الشّكل، وتكون ثُنائيّة الأبعاد، فمساحة المستطيل هي ناتج ضرب طوله بعرضه، ويُعبَّر عنها بالقانون الآتي:[٩]
مساحة المستطيل=الطول×العرض
أمثلة على مساحة المستطيل
مثال (1): مستطيل طوله 8سم، وعرضه 3سم. جِد مساحته.[٩]
الحلّ: بتعويض المُعطَيات في قانون مساحة المستطيل، فإنَّ الناتج يكون كما يأتي: مساحة المستطيل=8×3 مساحة المستطيل=24سم2
مثال (2): مستطيل مساحته 12سم2، وعرضه 3سم. جِد طوله.[٩]
الحلّ: بتعويض المُعطَيات في قانون مساحة المستطيل، تبقى القيمة المجهولة هي الطول: مساحة المستطيل=الطّول×3 12=الطول×3 وبقسمة طرفَي المعادلة على العدد 3، فإنَّ الناتج سيكون: الطول=4سم
متوازي المُستطيلات
متوازي المُستطيلات هو عبارة عن شكل هندسيٍّ، يشبه في شكله الصّندوق، وزواياه جميعها قائمة، ولهذا الشّكل ستّة أوجه مُستوية مُستطيلة الشّكل، وكلّ وجهين مُتقابلين فيه متطابقان، ولكنّ الأوجه المُتجاورة تكون ذات أبعادٍ مُختلفة، ولمتوازي المستطيلات اثنتا عشرة حافّةً، لكلّ ستّة حوافٍ بُعد مختلف عن الستّة المُتبقّية، ويُمكن اعتبار هذا الشّكل منشوراً، حيثُ إنَّه عبارة عن منشور مُستطيل، ويوجد متوازي المُستطيلات في عدّة أماكن في حياة الإنسان، ومن هذه الأماكن: البنايات، والصّناديق، والغُرف.[١٠][١١]
المراجع
- ↑ "Quadrilaterals", MathIsFun, Retrieved 14-3-2017. Edited.
- ^ أ ب "Rectangle", TutorVista.com, Retrieved 24-2-2017. Edited.
- ↑ "Rectangle", Math Open Reference, Retrieved 24-2-2017. Edited.
- ^ أ ب "Perimeter", MathGoodies, Retrieved 24-2-2017. Edited.
- ^ أ ب "Calculating the area and the perimeter", Math Planet, Retrieved 24-2-2017. Edited.
- ↑ "Perimeter of a Rectangle", mathteachers.co.au, Retrieved 24-2-2017. Edited.
- ^ أ ب "How to Find the Perimeter of a Rectangle: Formula & Example", Study.com, Retrieved 24-2-2017. Edited.
- ^ أ ب ت ث "Perimeter of a rectangle", Basic-Mathematics.com, Retrieved 24-2-2017. Edited.
- ^ أ ب ت "Area of a Rectangle", Math Goodies, Retrieved 14-3-2017. Edited.
- ↑ "Cuboids", TechnologyUK, Retrieved 24-2-2017. Edited.
- ↑ "Cuboids, Rectangular Prisms and Cubes", MathIsFun, Retrieved 24-2-2017. Edited.
المقالات المتعلقة بما محيط المستطيل
