قانون متوازي الأضلاع

محتويات

• ١ متوازي الأضلاع
• ٢ خصائص متوازي الأضلاع
• ٣ مساحة متوازي الأضلاع
• ٤ محيط متوازي الأضلاع
• ٥ حالات خاصة من متوازي الأضلاع

متوازي الأضلاع

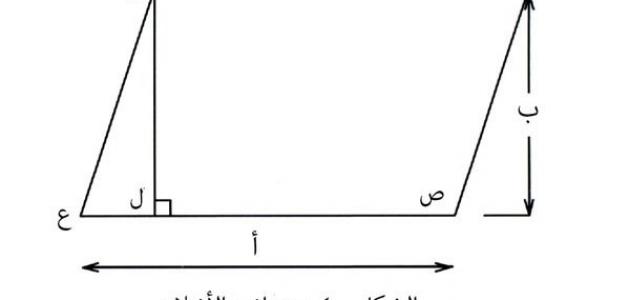
متوازي الأضلاع هو شكلٌ هندسيٌ مكونٌ من أربعة أضلاع، فيه كل ضلعين متقابلين متساويان في الطول ومتوازيان، أما قطرا متوازي الأضلاع، فكلٌّ منهما ينصّفُ الآخر، ومجموع زوايا المتوازي هي 360 درجة مقسمة إلى أربعِ زوايا، بحيث أنّ كلَّ زاويتين متقابلتين متساويتان.

خصائص متوازي الأضلاع

• قطرا متوازي الأضلاع ينصّف كلاًّ منهما الآخر.
• قطرا متوازي الأضلاع يتقاطعان في نقطةٍ تسمّى مركز متوازي الأضلاع.
• مساحة متوازي الأضلاع هي عبارة عن مساحة المثلثين المشكّلين من الأضلاع والقطرين.
• كل متوازي أضلاع له أربعة رؤوس.
• كل زاويتين متحالفتين مجموعهما يساوي 180 درجة.

مساحة متوازي الأضلاع

بما أن كل ضلعين متقابلين في متوازي الأضلاع متساويان، فهذا يجعل متوازي الأضلاع مكوناً من مثلثين متطابقيْن، ومساحة متوازي الأضلاع هي عبارةٌ عن ضعف مساحة المثلث المكوّن من ضلعين وقطر المتوازي، وبما أن مساحة المثلث = 1/2 * القاعدة * الارتفاع، فإن مساحة متوازي الأضلاع = 2 * مساحة المثلث مساحة متوازي الأضلاع = طول القاعدة * الارتفاع أمثلة:

• متوازي أضلاع طول قاعدته يساوي 10 سم، وارتفاعه يساوي 5 سم، احسب مساحته.

الحل: مساحة متوازي الأضلاع = طول القاعدة * الارتفاع

= 10 * 5 = 50 سم².

• متوازي أضلاع مساحته تساوي مساحة مربع طول ضلعه 4 سم، وارتفاعه 2 سم، احسب طول قاعدته.

الحل: مساحة المربع = الضلع² = 4² = 16سم²

مساحة المتوازي = مساحة المربع = 16 سم² طول القاعدة = مساحة متوازي الأضلاع / الارتفاع = 16 / 2 = 8 سم.

محيط متوازي الأضلاع

محيط متوازي الأضلاع هو عبارة عن مجموع أطوال أضلاعه الاربعة. محيط متوازي الأضلاع = 2 * (طول الضلع الأكبر + طول الضلع الأصغر) أمثلة:

• متوازي أضلاع طول ضلعه الأكبر يساوي 8 سم، وطول ضلعه الأصغر يساوي 6 سم، احسب محيطه.

الحل: محيط متوازي الأضلاع = 2 * (طول الضلع الأكبر + طول الضلع الأصغر)

= 2 * ( 8 + 6) = 2 * 48 = 96 سم

• متوازي أضلاع محيطه يساوي 24 سم، وطول ضلعه الأصغر يساوي 5 سم، احسب طول ضلعه الأكبر.

الحل: 2* طول الضلع الأكبر يساوي = 24 - (2*5)

= 24 - 10 =14 طول الضلع الأكبر = 14 / 2= 7سم.

• متوازي أضلاع طول ضلعه الأكبر يساوي 5 سم، وطول ضلعه الأصغر يساوي 5 سم، احسب محيطه.

الحل: بما أن طول الضلع الأكبر يساوي طول الضلع الأصغر، فهذا مربع محيط المربع = 4 * طول الضلع

= 4 * 5 = 20 سم.

حالات خاصة من متوازي الأضلاع

• إذا كانت إحدى زوايا متوازي الأضلاع قائمة، فذلك يعني أن بقية زواياه قائمة وهنا يصبح الشكل مستطيلاً.
• إذا كان قطرا متوازي الأضلاع متعامديْن، أو إذا كان هناك ضلعان متجاوران متساويان في الطول يصبح الشكل معيناً.
• إذا تواجدت كل الصفات السابقة المذكورة في متوازي الأضلاع، يصبح مربعاً.