قانون مساحة نصف الدائرة

محتويات

• ١ الدائرة
• ٢ مساحة الدائرة
• ٣ مصطلحات خاصة بقوانين الدائرة
• ٤ كيفية قياس مساحة نصف الدائرة

الدائرة

تعرّف الدائرة على أنّها إحدى الأشكال الهندسيّة المُنتظمة، وما يميّز الدائرة هو أنّها تخلو من الأضلاع لذلك فإننا لا نلاحظ أن لها أي زوايا، لكن الواقع هو أن للدائرة زاوية واحدة لها ضلعان وهميان؛ فالضلع الأول يكون عند نقطة دوران المحور حول نفسه والضلع الثاني يكون عند انتهاء دوران نفس المحور، لذلك فإنّ قياس زاوية الدائرة ثلاثمئةٍ وستين درجة، وتنشأ الدائرة عن طريق دوران المحور حول النقطة المركزية وتُسمّى مركز الدائرة، أمّا هذا المحور فيُسمّى نصف قطر الدائرة، وبناءً على ما سبق نستطيع استخراج قوانين الدائرة من خلال قياس طول نصف قطر الدائرة بما في ذلك قانون مساحة نصف الدائرة.

مساحة الدائرة

إنّ مساحة الدائرة هي المنطقة المحصورة داخل محيط الدائرة، وهي عبارة عن قرصٍ يُسمّى الدائرة، ولقياس مساحة الدائرة فإننا نحتاج إلى دراية تامّة بقانون مساحة الدائرة والذي يُعبّر عن مساحة هذا القرص بأيّ من وحدات قياس المساحة، وهي الملمتر المربع، والسنتمتر المربع، والمتر المربع،...

مصطلحات خاصة بقوانين الدائرة

• الشعاع: وهو مصطلح يُعبّر عن نصف قطر الدائرة.
• قطر الدائرة: وهو القطعة المستقيمة التي تصل نقطتين متقابلتين على محيط الدائرة مروراً يُمركز الدائرة.
• القوس: وهو جزء من محيط الدائرة.
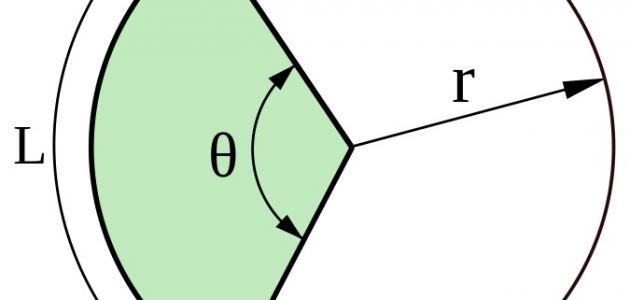
• القطاع: وهو المساحة المحصورة بين شعاعين.
• وتر الدائرة: وهو القطعة المستقيمة التي تصل بين نقطتين على محيط الدائرة دون المرور بالمركز.
• مركز الدائرة: وهو النقطة التي تتوّسط الدائرة وعادة تتخذ هذه النقطة الرمز (م) اختصاراً لكلمة (مركز) الدائرة.
• المماس: وهو المستقيم الذي يقطع الدائرة بنقطة واحدة فقط ويكون امتداده خارج الدائرة.

كيفية قياس مساحة نصف الدائرة

هناك قانون ثابت لقياس مساحة الدائرة ككل، لكن بما أنّ المطلوب هو معرفة مساحة نصف الدائرة ففي هذه الحالة يُقسم ناتج تطبيق قانون مساحة الدائرة على العدد اثنين، وقانون مساحة نصف الدائرة كالتالي:

• مساحة الدائرة= (طول نصف القطر)2×π

وπ هي قيمة ثابتة تساوي 3.14

• مساحة نصف الدائرة= ((طول نصف القطر)2 × π/2)

(طول نصف القطر× π/ 2)

مثال تطبيقيّ

لديك طاولة وسط ذات شكلٍ دائريّ، تريد معرفة مساحتها لشراء غطاء لها، إذا عرفت أنّ قطرها يساوي 100 سنتمترٍ، فاحسب نصف مساحة هذه الطاولة.

• المعطيات: قطر الدائرة يساوي 100 سنتمترٍ، إذاً نصف القطر هو 100/2= 50 سنتمتراً.
• الحلّ: مساحة الدائرة= (طول نصف القطر)2×π

مساحة الدائرة= (50)2×3.14= 7850 سنتمتراً مربعاً. مساحة نصف الدائرة= مساحة الدائرة/ 2 مساحة نصف الدائرة= 7850/ 2= 3925 سنتمتراً مربعاً.