قانون حجم الدائرة

محتويات

• ١ تعريف الدائرة
• ٢ قانون مساحة الدائرة
• ٣ قانون حجم الدائرة
• ٤ خصائص الدائرة

تعريف الدائرة

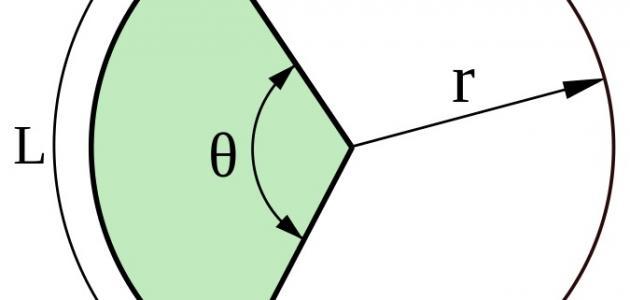
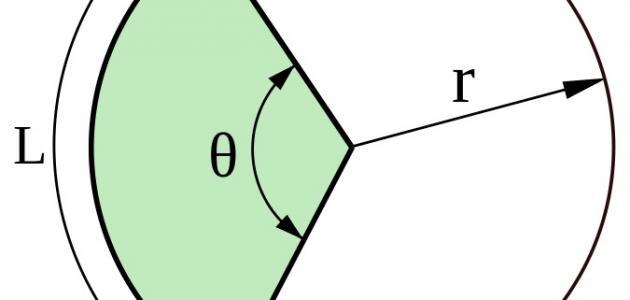
هي مجموعةُ نقاطٍ كثيرةٍ تدورُ حول نقطةٍ ثابتةٍ تسمّى مركزاً، وتبعد عنها بعداً ثابتاً، والمسافة بين أيّ نقطة من هذه النقاط والمركز تعرف بنصف القطر، ووتر الدائرة هو المسافة بين أيّ نقطتين على محيط الدائرة. وهناك حالةٌ خاصّةٌ من الوتر، هي القطر وهو القطعة المستقيمة الواصلة بين نقطتيْن على محيط الدائرة مارّة بالمركز.

للدائرةِ قانونان يُستخدمان في العمليّات الحسابيّة هما مساحة الدائرة ومحيط الدائرة، ولا يوجدُ للدائرة حجمٌ؛ لأنّ الدائرة شكلٌ هندسيٌ ثنائي، وكل الأشكال الثنائية الأبعاد لها مساحةٌ ومحيطٌ فقط وليس لها حجمٌ، أمّا الأشكال الهندسيّة ثلاثية الأبعاد فهي التي يكون لها حجمٌ، وبالتالي ليس للدائرة إلا قانون مساحةٍ محيطٍ، وسنذكرُهما مع الشرح هنا.

 

قانون مساحة الدائرة

لقد جاءت كلمة مساحة من الفعل مسح ويعني تمرير شيءٍ على شيءٍ آخر، ومساحة الدائرة تعني تغطية كلّ النقاط التي هي داخل الدائرة.

مساحة الدائرة = نق2×ط حيث نق هي نصف القطر، وط عبارة عن ثابت يساوي 3.14 أو 22/7.

• مثال: إذا كان طول قطر دائرةٍ ما 46 سم، احسب مساحتها. الحلّ:

طول نصف القطر=القطر/2. =46/2 =23سم. مساحة الدائرة=نق²ط. =23²×3.14 =529×3.14 =1661.06سم².

 

قانون حجم الدائرة

محيط الدائرة=2نق×ط.

• مثال: إذا كان طول نصف قطر عجل سيارة ما يُساوي 15 سم، احسبْ محيط جميع عجلات السيارة بالمتر. الحلّ:

محيط الدائرة=2نق×ط. =2×15×3.14 =30×3.14

94.2سم.

 

خصائص الدائرة

• الوتر هو الخطّ المستقيم الواصل بين أيّ نقطتين موجودتين على الدائرة، ولا يشترطُ في هذا الخطّ المرور بالمركز.
• هناك علاقةٌ تربطُ القطر بالمحيط وهي: (محيط الدائرة ÷ قطرها = 3.14 تقريباً). الرقم 3.14 يسمّى نسبةً تقريبيّةً ويرمز له بالرمز بايπ أو ط، وسمّيت نسبةً لأنّها تعبّر عن علاقة بين القطر والمحيط، وهي ثابتةٌ لكلّ الدوائر مهما كان حجمها.
• القطر هو أكبر وترٍ في الدائرة، ونقول إنّ كلّ قطرٍ وترٍ ولكن ليس كلّ وترٍ قطر.
• محيط أي دائرةٍ يساوي تقريباً ثلاثة أضعاف طول قطرها.
• قوس الدائرة هو جزءٌ من المحيط يعتمدُ طوله على نصف قطر الدائرة والزاوية التي تقابله.
• عندما تدورُ أيّ دائرةٍ حول قطرٍ من أقطارها ينتجُ عن هذا الدوران شكلٌ ثلاثيّ الأبعاد هو الكرة، وكون نصف قطرها هو نصف قطر الدائرة، ولكن مساحة الكرة مختلفةٌ عن مساحة الدائرة، والمختلف أيضاً أنّ الدائرة ليس لها حجم لأنّها شكلٌ ثنائي الأبعاد ولأنّها تقع في مستوىً واحد، بينما الكرة لها ثلاثة أبعاد وتقعُ في ثلاثة مستويات.