خصائص متوازي الأضلاع

محتويات

• ١ متوازي الأضلاع
  • ١.١ خصائص متوازي الأضلاع
  • ١.٢ مساحة ومحيط متوازي الأضلاع
  • ١.٣ الحالات الخاصة في متوازي الأضلاع
  • ١.٤ شروط الشكل الرباعي ليكون متوازي أضلاع

متوازي الأضلاع

يمكننا تعريف متوازي الأضلاع على أنه شكل هندسي رباعي الأضلاع، حيث يكون كل ضلعين متقابلين من أضلاعه متوازيين، وكل ضلعين متوازيين منه يكونان متساويين بالطول بالإضافة إلى أن كل زاويتين متقابلتين من زواياه تكونان متساويتين، كما أن قطريه ينصفان بعضهما البعض، ومجموع زواياه الأربعة يساوي (360) درجة، يُطلق على متوازي الأضلاع بأنه شبيه المعين في شكله.

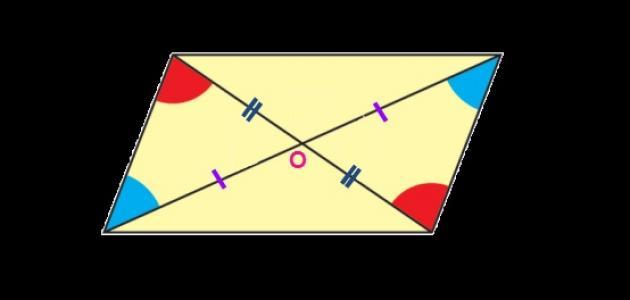
خصائص متوازي الأضلاع

• يتميّز متوازي الأضلاع بأن كل قطر من أقطاره منصف للقطر الآخر.
• تساوي مساحة متوازي الأضلاع ضعف مساحة المثلث والذي يتألف من ضلعين وقطر واحد.
• تتقاطع أقطار متوازي الأضلاع في نقطة تكون مركز تناظر لمتوازي الأضلاع، ويطلق على هذه النقطة " مركز متوازي الأضلاع".
• يقسم متوازي الأضلاع إلى شكلين هندسيين متطابقين.
• يتميّز بأن كل زاويتين من زواياه المتقابلة تكون متساوية.
• يتصف متوازي الأضلاع بأن كل ضلعين من أضلاعه المتقابلة متساوية في المقدار.

مساحة ومحيط متوازي الأضلاع

عندما نفترض أن مساحة متوازي الأضلاع هي (r)، يمكن حساب مساحة متوازي الأضلاع بواسطة معرفة طول كل من الارتفاع والقاعدة وذلك من خلال القانون التالي : r = bh، حيث إن (h) تمثل الارتفاع، وهو عبارة عن المستقيم النازل من الرأس المقابل للضلع الذي عليه، و(h) تُمثل طول القاعدة وهي عبارة عن أي ضلع من أضلاع متوازي الأضلاع.

يمكننا احتساب المساحة أيضاً بمعرفة أطوال ضلعين متجاورين وقياس الزاوية بينهما بواسطة القانون التالي: r =ab.sin(x، حيث إن aوb هما طولا الضلعين المتجاورين فيه بالإضافة لقياس أية زاوية فيه.

كما يُمكن حساب المساحة من خلال معرفة أطوال القطرين وقياس أية زاوية من زواياه المحصورة بين القطرين بالقانون التالي: (r=mn.sin(x)\frac (1) (2 ، حيث إن n ،m هما أطوال القطرين، x هي قياس أية زاوية من الزوايا المحصورة بينهما.

أما محيط متوازي الأضلاع فيمكن حسابه بواسطة العلاقة: (p=2(a+b ، حيث إن aو b يُمثلان أطوال أي ضلعين متجاورين في المتوازي.

الحالات الخاصة في متوازي الأضلاع

• في حال تعامدت أقطاره أو تساوت أطوال الضلعين المتجاورين يعتبر هذا الشكل معيناً.
• في حال تساوت أقطاره أو في حال كانت إحدى زواياه بشكل قائم يعتبر الشكل مستطيلاً.
• في حال كان الشكل الهندسي معيناً ومستطيلاً في نفس الوقت فيكون هذا الشكل مربعاً.

شروط الشكل الرباعي ليكون متوازي أضلاع

• في حال كان الضلعان المتقابلان متطابقين.
• عندما يتضمن الشكل الرباعي ضلعين متطابقين ومتقابلين ومتوازيين في آن واحد.
• في حال كانت أقطاره تنصف بعضها.
• عندما تتساوى زواياه المتقابلة.
• عندما يكون مجموع كل زاويتين من زواياه المتحالفة بضلع واحد تساوي (180) درجة.