
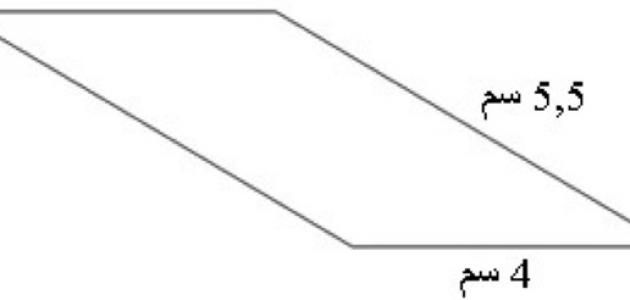
عالم الرياضيات والأشكال مليءٌ بالمضلعات والأشكال الهندسيّة المختلفة التي اكتشفت على مر العصور، وساعدت تلك الأشكال المهندسين والرياضيين والفيزيائيين في علومهم من تصميمٍ وبناءٍ واشتقاق قوانين وحلّ مشاكل علميّة كثيرة.
محتويات- ١ متوازي الأضلاع
- ٢ قوانين مهمّة
- ٣ رسم متوازي الأضلاع
- ٣.١ الأدوات المستخدمة
- ٣.٢ طريقة الرسم
من الأشكال الهندسيّة المعروفة المهمة هو شكل متوازي الأضلاع وهو شكلٌ مضلعٌ رباعي ومن اسمه نستنتج أنه يحتوي على أربعة أضلاع، ثنائي الأبعاد، وأهمّ ما يميّز هذا الشكل هو أنه كل ضلعين متقابلين متوازيين متساويين، وبالتالي وحسب قانون الجيب فإنّ كل زاويتين متقابلتين متساويتين ومجموعهما 180 درجة ومجموع زواياه الأربعة كأي شكل رباعي 360 درجة، وبالتالي فإنّ القطران ينصف كلٌ منهما الآخر ويتقاطعان في نصف كل قطر.
قوانين مهمّةعند تنصيف متوازي الأضلاع ينتج مثلثان قائما الزاوية يتشاركان في الارتفاع، ومن هذا نستطيع استنتاج أن مساحته تساوي مجموع مساحتي المثلث:
- مساحة المثلث = 0.5×القاعدة×الارتفاع.
- مساحة متوازي الأضلاع= 2×(مساحة المثلث) حيث المثلثان متماثلان، وبالتالي مساحة متوازي الأضلاع تساوي.
- مساحة متوازي الأضلاع= القاعدة×الارتفاع.
- إيجاد ارتفاع المتوازي: طول القاعدة معروف أمّا الارتفاع، فيتمّ إيجاده من خلال اسقاط خطٍ عمودي من نقطةٍ مقابلةٍ للقاعدة (الرأس منفرج الزاوية)، فينتج مثلث قائم الزاوية وتره هو ضلع متوازي الأضلاع الذي يكون معلوم، ومن خلال قوانين مثلث قائم الزاوية وقوانين الزوايا، وأنّ الارتفاع يكون مقابل الزاوية فإنّ الارتفاع= الوتر×جا (الزاوية الحادّة).
- أما محيط متوزاي الأضلاع، فهو مجموع أضلاعه الأربعة كباقي الأشكال الرباعيّة الهندسيّة .
يستخدم متوازي الأضلاع بكثرة في المخططات الهندسية لذلك من المهم معرفة كيفية رسمه
الأدوات المستخدمة- المنقلة.
- الفرجار.
- المسطرة.
في البداية نرسم قاعدة متوازي الأضلاع، ثم نضع المنقلة على أحد طرفي القاعدة ونعين الزاوية المطلوبة، من الطرف نفسه نقوم بمد خطٍ بقياس الزاوية التي تم تحديدها، ثمّ على امتداد ذلك الخط نحدد الطول المطلوب، الآن أصبح لدينا طرفين من متوازي الأضلاع، من طرف الضلع الذي بالزاوية نفتح الفرجار بطول القاعدة ونركزه على النقطة الحرة ونرسم قوس، ومن القاعدة نفتح الفرجار بطول الضلع ونرسم قوساً آخر، نقطة التقاء القوسين هي النقطة الرابعة لمتوازي الأضلاع فنرسم باستخدام المسطرة خط من القاعد والضلع وبهذا ينتج متوازي الأضلاع. مع تطوّر التكنولوجيا والبرامج الحاسوب الهندسية فاليوم نستطيع رسم متوازي الأضلاع بسهولة من خلال الحاسوب باستخدام برنامج الأوتوكاد الخاص بالمهندسين وتكون الدقة فيه أعلى من الرسم الهندسي اليدوي التقليدي.
المقالات المتعلقة بمساحة متوازي الأضلاع