قانون حساب مساحة الدائرة

محتويات

• ١ الدائرة
• ٢ اشتقاق قانون مساحة الدائرة
• ٣ كيفية حساب مساحة الدائرة
• ٤ محيط الدائرة

الدائرة

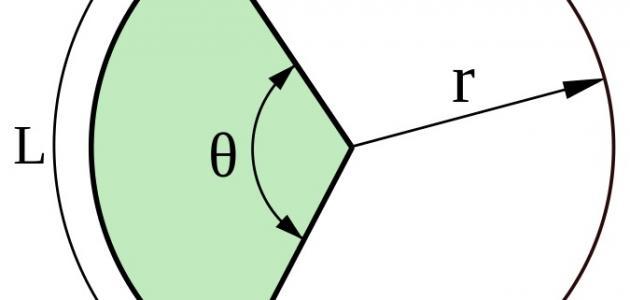
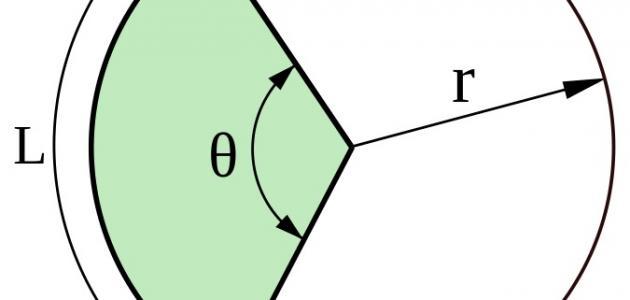
الدائرة شكل من الأشكال الهندسيّة البسيطة، وهي مجموعة من النقاط المتّصلة مع بعضها البعض، وتقع على بعد ثابت من نقطة ثابتة، يطلق عليها مركز الدائرة، والمسافة بين النقاط ومركز الدائرة عبارة عن نصف القطر، وتشكل النقاط متصلةً مع بعضها محيط الدائرة.

 

اشتقاق قانون مساحة الدائرة

يتم حساب مساحة الأشكال بشكل عام من خلال حاصل ضرب الطول في العرض، وبما أنّ الدائرة لا تحتوي على أضلاع، ولحساب قانون مساحة الدائرة صنع العلماء دائرة من الورق المقوّى، وتم تقطيع الدائرة إلى 8 أجزاء، وإلصاق هذه الأجزاء على شكل المستطيل، وبعدها تم قياس مساحة هذا المستطيل، ووجد العلماء أنّ الطول يساوي نصف محيط الدائرة، أما العرض فكان مساوياً لنصف القطر، وبالتالي تكون مساحة الدائرة مساويةً لمساحة المستطيل المصنوع منها، أي أنّ مساحة الدائرة= نصف المحيط × نصف طول القطر، وعند صياغة هذا القانون بدلالة نصف القطر، يمكننا تعويض محيط الدائرة(القطر * pi)، وبالتالي يصبح قانون المساحة كالآتي:

• مساحة الدائرة = ½ (pi * القطر) * نصف القطر = ½ القطر * نصف القطر * pi = نصف القطر * نصف القطر * pi
• إذاً مساحة الدائرة = pi * (نق)2

 

كيفية حساب مساحة الدائرة

• أولاً، يجب حساب طول نصف القطر: يتم قياس طول القطر بالمسطرة، والقطر هو المسافة بين نقطة من أحد جوانب الدائرة حتى نقطة مقابلة في الجانب الآخر، حيث يتم تقسيم القطر على 2 للحصول على نصف القطر.
• ثانياً، تعويض قيمة نصف القطر في قانون مساحة الدائرة كالأتي:
  • مساحة الدائرة = pi * نق2، حيث pi قيمة ثابتة ومقدارها 3.14، ونق2، مربع نصف القطر.
• مثال (1): أوجد مساحة الدائرة التي نصف قطرها 5سم؟
• الحل: مساحة الدائرة = pi * نق2 = 3.14 * 25 = 78.5 سم2
• مثال (2): أوجد نصف قطر الدائرة التي مساحتها 314 سم2؟
• الحل: مساحة الدائرة = 3.14 * نق2، 314 = 3.14 * نق2، إذاً نق2 = 100، ونصف القطر = 10سم.

 

محيط الدائرة

لقياس محيط الدائرة صنع العلماء دائرة من خيط، وبعد فك الخيط تم قياس طول الخيط، واستنتج العلماء أنّ محيط الدائرة هو طول الخيط المفكوك، وعند تكرار العمليّة مرةً أخرى، وعلى دوائر أخرى، وجد أنّ النسبة بين محيط الدائرة أو طول الخيط المفكوك على القطر نسبةً ثابتةً، وبقسمة محيط الدائرة على قطرها، ينتج رقم ثابت وهو 3.14، والذي أطلق عليه لاحقاً pi، كما أثبت العلماء في حال كان قطر الدائرة يساوي واحداً، فإن محيطها يساوي pi، وبعلاقة رياضيّة، محيط الدائرة = طول القطر * pi.

• مثال (3): أوجد محيط الدائرة التي قطرها 7سم؟
• الحل: محيط الدائرة = طول القطر * pi ، محيط الدائرة = 22سم.